Trigonometry Functions

Aspen Graphics 4.0 trigonometry functions accept arguments in degrees or radians. Aspen’s trigonometry functions include:

There are two common measures for angles: degrees and radians. Degrees, the more familiar measure, are derived by dividing a circle into 360 equal units such that a right angle is at 90. A radian, on the other hand, requires you understand the "unit circle":

:

The unit circle is a circle with a radius of 1 whose center is the vertex of the angle in question (see X in the figure above). A radian is the arc length of the unit circle. (It is possible to measure the radian of any circle by calculating the ratio of the arc length to the radius.)

It is easy to convert between degrees and radians. Conversion from degrees to radians is,

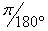
Conversion from radians to degrees is,

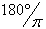
If you are working in degrees, use the degree functions. Similarly, if you are working in radians, use the radian functions. Passing degrees to a radian function can give undesirable results.

Trigonometry Overview

OK, trig functions. Why? The simple answer is, angles. With Trigonometry functions, you can ask, “What is the angle between an instrument’s 52-week high and its current price?” In the following figure, notice the placement (artificial) of the unit circle at the 52-week high.

The example that follows identifies the vertex angle, where the unit circle is rendered in the figure above.

With Aspen's trigonometry functions and Pythagorean theory, you can determine all three angles in a right triangle, including the vertex angle (0,0 on the X,Y axis). Orient yourself to the right triangle rendered in trend lines above.

To accomplish this, you need to identify the slope of the hypotenuse, which is:

The Rise

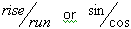
The rise is the difference between the 52-week high and the last price. To determine the 52 week high, use the .hi52 extension on feeds that support fundamental data. Alternatively, use the RMAX() function:

e52WeekHigh(instrument)=begin

retval = vchart(rmax(i.high,1,eDaysSinceHigh($1)) + 1)

end

where:

vchart=chart($1,DAILY_WIDTH,DAY_BAR,STANDARD_PREFETCH,DAY_ONLY)

and,

DAY_ONLY=3

STANDARD_PREFETCH=200

DAILY_WIDTH=1

DAY_BAR=2

and,

eDaysSinceHigh(instrument)=begin

retval = vchart(disttomax(instrument.high,1,abs(eLookBack)))

end

and,

eLookBack=begin

retval = abs(BusDays(date,AddYears(date,-1)))

end

eDaysSinceHigh() returns the number of days between today and the 52-week high.

eLookBack() returns the number of business days between today, and today’s date one year ago.

e52WeekHigh() returns the highest high in the range from the current bar to the bar that is eDaysSinceHigh() bars back.

With the highest high in this range, the rise is the difference between the identified high and the current last price:

ePriceDiff(instrument)=begin

retval = e52WeekHigh(instrument) - instrument.last

end

The Run

The run is the distance in periods between today’s date and the date of the 52-week high. The number of periods is determined by the time base of the chart() function. Look to the vchart() definition above. vchart() is merely a chart() function defined by formula values.

The chart() function defines periods in two arguments: base, and length. Here, vchart()’s DAY WIDTH argument has a value of 1, and its DAY_BAR argument a value of 2 (0 being tics, 1 being 15-minute, and 2 being Day), hence 1 day. To determine the run, use the DISTTOMAX() function:

eDaysSinceHigh(instrument)=begin

retval = vchart(DISTTOMAX(instrument.high,1,eLookBack))

end

The value returned by eDaysSinceHigh() is the distance, in days, between the 52-week high and today. This value is the run, or cosine.

The Slope

With the rise and run defined, the slope of the hypotenuse can be determined as rise/run.

eSlope(instrument)=begin

y = eDaysSinceHigh(instrument)

x = -(ePriceDiff(instrument))

retval = x / y

end

The Angle

To identify the angle, call ArcTangent() with the return value of the eSlope() formula.

eAngle(instrument)=begin

retval = vchart(arcTangent(eSlope(instrument)))

end