|
|

In 1973, Fischer Black and Myron Scholes developed the Black/Scholesí model to evaluate European call options. In 1976, Fischer Black modified the Black/Scholesí model to apply it to futures options. Blackís modified model became known as the Black model. Since then, other mathematical models designed to help traders understand the world of options have emerged.
Aspen Graphics uses a generalized version of the Black/Scholesí model that can be used to model future options (Black) and foreign currency options (Garman Kohlhagen), as well as stock and index options (Black/Scholesí).
Formula:
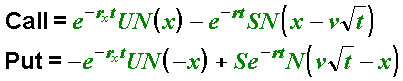
Delta
A common way to trade options is to hedge an options position against a position in the underlying market. In measuring Delta, the hedge relationship between an underlying instrument and an option is inverse. If one increases, the other decreases and vice versa. Such a hedge is not influenced by the direction of movement in the underlying contract. A trader uses a hedge ratio to establish this kind of hedge. The hedge ratio is also know as the Delta.
A Delta is a number between -100 and 100. Deltas range from zero for far out-of-the-money calls to 100 for deeply in-the-money calls. Deltas range from zero for far out-of-the-money puts to -100 for deeply in-the-money puts. At-the-money calls have Deltas of about 50 while at-the-money puts have Deltas of about -50. Increasing the volatility causes all call Deltas to move toward 50 and all put Deltas to move toward -50. The underlying contract always has a Delta of 100.
Formula:
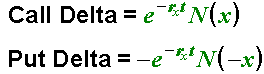
Gamma
The Gamma is sometimes referred to as the curvature of an option. Gamma is the rate at which an option gains or loses Deltas as the underlying contract moves up or down. The Gamma is given in Deltas-per-point-change in the underlying contract. If the underlying contract moves down, the Gamma number from the old Delta is subtracted to derive the new Delta. Conversely, if the underlying contract moves up, the Gamma number from the old Delta is added to derive the new Delta. All futures calls and puts have a positive Gamma.
All at-the-money options always have a greater Gamma than either in-the-money or out-of-the-money options with the same expiration date. As time to expiration grows shorter, or as volatility is decreased, the Gamma of at-the-money options can increase dramatically.
Formula:
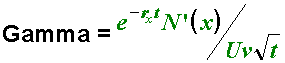
Theta
The Theta is a measure of the effect of a change in time to expiration on the theoretical values of puts and calls. The Theta is sometimes referred to as the time decay factor because it measures the rate at which an option loses its value as time passes. The Theta of an at-the-money option always increases as expiration approaches, so a short term at-the-money option will always decay more quickly than a long term at-the-money option. The at-the-money option always has a greater Theta than either an in-the-money or an out-of-the-money option with the same expiration date.
Formula:

Vega
The sensitivity of an optionís theoretical value to a change in interest rates is given by Rho. All futures options have a negative Rho. Increasing interest rates decrease the value of an option because it costs more to carry the option position. Rho is generally not used to choose an option strategy or manage risk on most futures; however, Rho often plays a role in identifying option strategies and in managing risk for stocks, currencies, and physical commodities because such instruments can be sensitive to interest rate changes.
Formula for Futures:
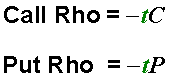
Where:
C = price of call.
P = price of put.
Formula for Non-Futures:
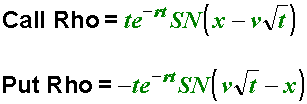
Formula for Foreign Currencies:
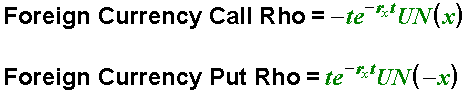
©2008 Aspen Research Group, Ltd. All rights reserved. Terms of Use.